Maria Conceição Leite's research   Page under construction...



  GOAL: Develop and apply mathematical methods that contribute for the
           understanding of complex natural systems.





Projects on Applications to Biological Sciences
Image Thumbnail
Some research topics I worked on in the area of mathemtical biology include ecology, epidemiology, and transcriptional regulatory networks. In most of these works, coupled systems of nonlinear ordinary differential equations were used to build mathematical models for the systems under study. I further investigate model dynamical properties and infer about biological mechanisms using a combination of dynamical systems techniques and numerical simulations. The research activity's resulting papers / preprints are the following:

1. M.C.A. Leite, S. Tang, X. Xiao, and M. Zhu, Climate-driven dynamics of seasonal influenza in subtropical and temperate regions. Preprint (2014).
2. B. Chen and M.C.A. Leite, Coupling discrete fire and insect outbreak disturbances in forests. Ecological Modelling, Accepted (2014).
3. Y.P. Wang, B.C. Chen, W.R. Wieder, M.C.A. Leite et al. Oscillatory behavior of two nonlinear microbial models of soil carbon decomposition. Biogeosciences, 11: 1817-1831 (2014).
4. M.C.A. Leite, N.P. Petrov, and E. Weng. Stationary distributions of a semistochastic process with disturbances at random times and random severity. Nonlinear Analysis: Real World Applications, 13:497-512 (2012).
5. Z. Feng,J. Velasco-Hernandez, B. Tapia-Santos, and M. C. A. Leite. A model for coupling within-host and between-host dynamics in an infectious disease. Nonlinear Dyn, doi:10.1007/s11071-011-0291-0 (2011).
6. J.X. Velasco-Hernandez and M.C.A. Leite. A model for a SEIR disease with social isolation. Salud Publica de Mexico, 53(1):40-47 (2011).
7. M.C.A. Leite and Y. Wang. Multistability, Oscillations and Bifurcations in Feedback Loops. Math. Biosc. Eng. 7(1) (2010).

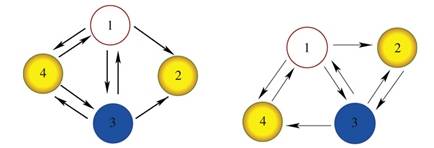
Projects on Theory of Coupled Cell Systems
Image Thumbnail

Besides the applied aspects of my research activity, I also develop the theory of coupled `cell' networks, where the `cell' is a system of nonlinear differential equations.
Networks arise naturally in many diverse fields and there are numerous examples in natural systems. Thus, it is important to increase our understanding of the principles that govern the dynamics of networks, which motivates my research project on the theory of coupled cell systems. A general question that we studied and would like to further investigate is: What aspects of the dynamics of coupled cell systems are due to network topology and what aspects are due to the details of individual differential equation? My research activity in this area resulted in the follow papers:

8. A. Arsie, M. Golubitsky, and M.C.A. Leite. Strongly Fedforward Neworks: Linear Structure and Bifurcations. In preparation.
9. M.A.D. Aguiar, A.P.S. Dias, M. Golubitsky, and M.C.A. Leite. Bifurcations from Regular Quotient Networks: A first Insight. Physica D 238 (2009) 137-155.
10. M.A.D. Aguiar, A.P.S. Dias, M. Golubitsky, and M.C.A. Leite. Homogeneous Coupled Cell Networks with S_3-symmetric Quotient. Discrete and Continuous Dynamical Systems Suplements (2007) 1-9.
11. M.C.A. Leite and M. Golubitsky. Homogeneous Three-cell Networks. Nonlinearity 19 (2006) 2313-2363.