and we want to graph 
and 
using 
The graph of 
is Example #1 (page 220): We have and we want to graph and using The graph of is
 |
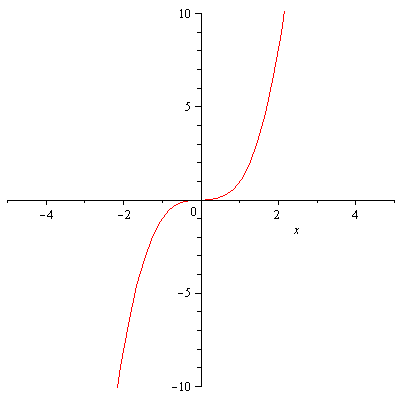According to our rules 
will shift 
down by 1 unit. The graph for 
is pictured below
 |
Notice that it is in fact a downward shift by one unit
To see what 
should look like we proceed in two steps. First, adding 2 inside the parenthesis will shift the graph of 
to the left 2 units.
 |
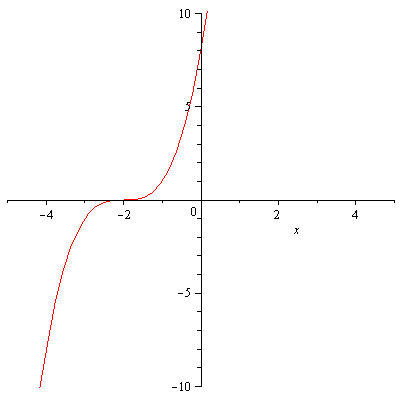Now the addition of 1 outside the parenthesis will shift the previous graph up by one unit.
 |
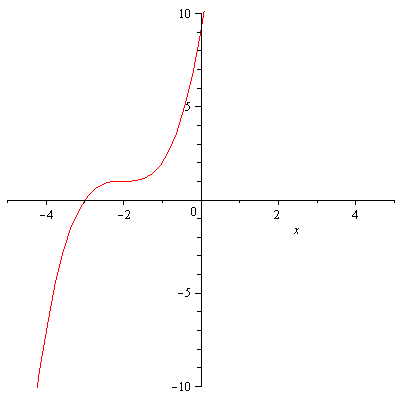Hence the graph of 
is the graph of 
shifted left two units then up one unit.
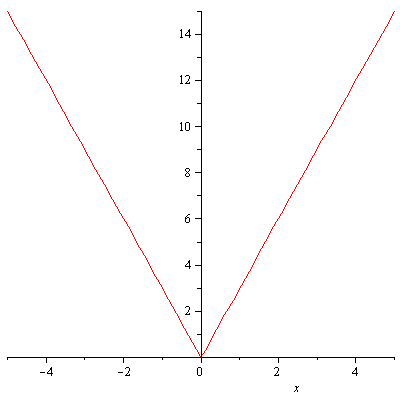
Example #4 (page 223): We have 
and we want to find 
and 
. The graph of 
is
 |
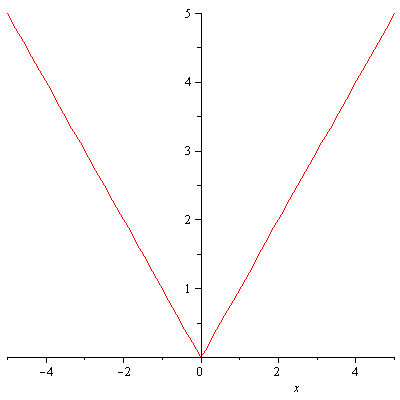Notice that we can write 
and 
Since the multiplication in both cases is happening away from the x our rules tell us that 
and 
will be vertical stretches/shrinks. Since 3>1 
will stretch 
vertically by 3 units (i.e. it will not affect the x-coordinates but all the y-coordinates will be multiplied by 3). Hence the graph of 
is
 |
This next picture contains the graphs of both 
and 
to clearly illustrate that a stretch has occured.
 |
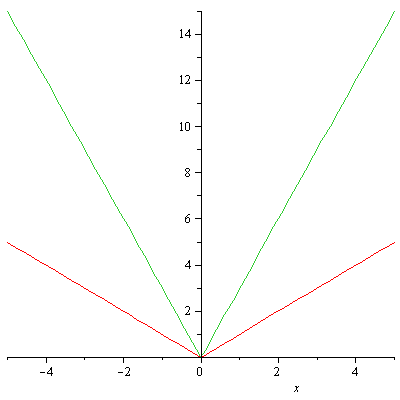The green graph is 
and the red graph is 
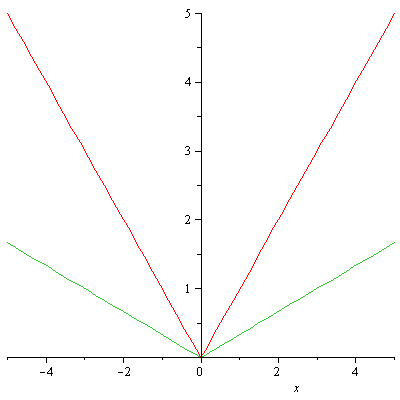
Following the same procedure outlined above the graph of 
will shrink 
by 1/3 in the vertical direction. The graphs of 
(red) and 
(green) are pictured below.
 |