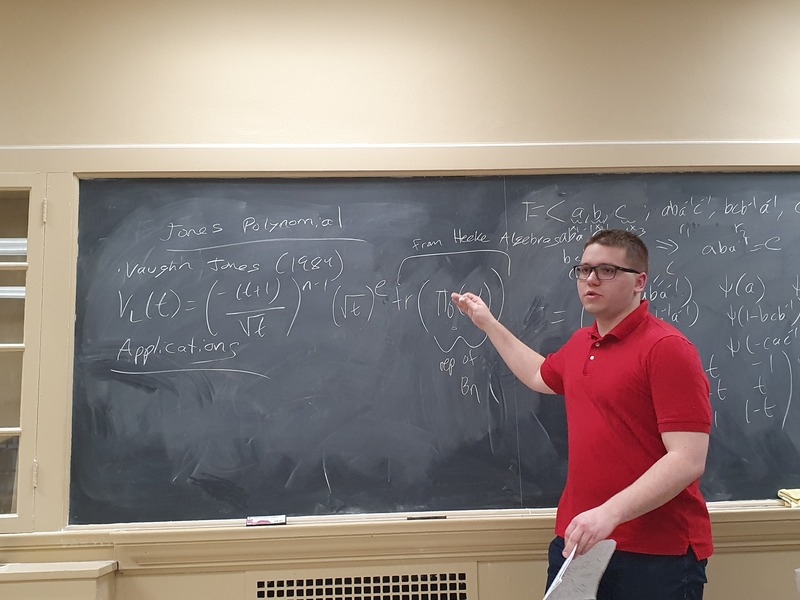For students: our AMS Graduate Chapter, student seminar, Delta X, and other interesting activities.
For undergraduate students (any major), we have Delta X math club.
In Spring 2023, we meet 4-5PM in the Math coffee room. We have two large events: Pie day, 3/14, 1.59PM, UH2060 and
Math Trivia, 4/14, 5-7PM, UH4480.
Snacks, prizes.
For graduate students, we have AMS graduate students chapter. In Spring 2023, it runs as snacks and research talks.
- Fall 2020, TBA. Yunus Zeytuncu, University of Michigan-Dearborn.
- April 29, 2020, 4pm-5pm, online. A talk by Brian Grove.
Title: Arithmetic Topology - From Knots to Primes.
Abstract: At first glance, Topology and Number Theory are two completely unrelated areas of mathematics. However, at the beginning of the 19th century, Gauss discovered a surprising connection between Quadratic Residues and Linking Numbers which started the development of Arithmetic Topology. The subject has since flourished with the help of tools from Algebraic Number Theory, Modern Algebraic Geometry, 3- Manifold Topology, etc. I will explain two main developments in this area, the Et'ale Fundamental Group and the Iwasawa Polynomial, the arithmetic analog of the Alexander Polynomial I discussed last time. Several examples will be given and if time permits I will state the Iwasawa Main Conjecture. - (Tuesday! unusual time) April 28, 2020, 4pm-5pm, online. A talk by Anthony Vasaturo, Trine University.
Title: On the "Equivalence" of g-Tori, Compact Riemann Surfaces, Smooth Projective Varieties, and Homogenous Coordinate Rings.
Abstract: Though mathematics is often taught to students compartmentalized neatly into distinct subjects such as Algebra, Analysis, and Topology, many of the most powerful fields of mathematics, such as Algebraic Geometry, require a remarkable amount of synthesis across various disciplines. This talk will highlight just one example displaying the beauty of such harmony: we will discuss the equivalence of spheres with g handles (g greater than or equal to 0), compact Riemann Surfaces, Nonsingular Projective Curves, and Finitely Generated k-Algebras which are also Integral Domains over an algebraically closed field k (often called Affine Coordinate Rings, a slight abuse of language). In this way, we will see that Topology, Complex Analysis, Geometry, and Algebra have, in some sense, a substantial amount of overlap. - April 15, 2020, 4pm-5pm, online. A talk by Sunil Khanal, PhD student.
(continuation of March 25 talk) Title: Matrix Representations of 9-Dimension Indecomposable Lie Algebras That Have a Non-Trivial Levi Decomposition II
- April 8, 2020, 4pm-5pm, online. A talk by Alessandro Arsie.
Title: Some ideas about deterministic chaos.
Abstract: In this talk, I will show how even very simple systems (like a periodically forced pendulum) can exhibit extremely complex dynamics, so complex that indeed they defy any possibility of prediction (which is one of the aspects of deterministic chaos). Here the lack of reliable predictions is not due to the limitations of the computing power in any simulation, but it is an intrinsic aspect of the system. The first intuition about this goes back to Poincare' with his insight about homoclinic phenomena. Later on, Smale showed that there is an underlying structure (nowadays called Smale's horseshoe) behind these phenomena, which is somehow the source of their complexity and unpredictability. Depending on the time availability, I will also discuss some other ideas related to this (like symbolic dynamics and hyperbolicity). - March 25, 2020, 4pm-5pm, online. A talk by Sunil Khanal, PhD student.
Title: Matrix Representations of 9-Dimension Indecomposable Lie Algebras That Have a Non-Trivial Levi Decomposition II
Abstract: I will give a very basic introduction to Lie Algebra without any prior knowledge and I will define types of Lie Algebra with several examples. Then I will define a representation of Lie Algebra (with examples). Finally, I will discuss representations of 9- Dimension indecomposable Lie algebras that have a non-trivial Levi decomposition. - March 4, 2020, 4pm-5pm, UH 2210. A talk by Brian Grove.
Snacks will be served at 3:30pm in the coffee room (UH2060).Title: Knots and Knot Invariants
Abstract: Classically, the idea of a knot was motivated by our intuition from the world around us. However, these simple closed curves in 3-space have applications in hyperbolic geometry, quantum field theory, and even number theory. I will provide the definition of a knot and give basic examples. Then I will discuss isotopy and the equivalence of knots. This will lead us to knot invariants, such as the Knot Group and Alexander Polynomial. - March 2, 2020, 5-8:30PM, UH 2060 and UH4410. Data Science at Dept. of Math and Stats unveiling event and Algebra Trivia.
Tshirts/food/algebra trivia! All students who like/curious about math of data/pure math/applied math/stats/ are cordially invited!!
Some nice refreshments: 5-6PM, UH 2060 (math coffee room)
Data Science at Dept. of Math and Stats unveiling event: 6-7PM, UH 4410
Algebra Trivia (we will be forming teams on the spot, you don't need to come with your own team): 7-8:30PM, UH 4410 - Feb. 19, 2020, 4pm, UH2210. A talk by Yagmur Yilmaz, PhD student.
Snacks will be served at 3:30pm in the coffee room (UH2060).Title: Persistent Homology (continuation)
Abstract: We will introduce basic concepts of persistent homology such as filtration, birth and death of homology classes, and persistent diagram. - Feb. 5, 2020, 4pm, UH2210. A talk by Yagmur Yilmaz, PhD student.
Snacks will be served at 3:30pm in the coffee room (UH2060).Title: Persistent Homology
Abstract: In this talk, we will explain some basic definitions of algebraic topology which are simplicial complex and homology groups. After that, we will introduce basic concepts of persistent homology such as filtration, birth and death of homology classes, and persistent diagram. - Dec. 4, 2019, 4pm, UH2210. (cont-d) A talk by Chanaka Kottegoda, a PhD student.
- Nov. 13, 2019, 4pm, UH2210. A talk by Chanaka Kottegoda, a PhD student.
Snacks will be served at 3:30pm in the coffee room (UH2060).Title: Dynamical systems and introduction to Bifurcations
Abstract: The aim of this talk is to serve as an introduction to dynamical systems and bifurcation theory without any prior knowledge. Hence using some basic definitions first we will define a dynamical system and give several examples. Then we will introduce the concept of bifurcation theory. Here we will talk about few bifurcations that we can see in dynamical systems such as saddle node bifurcation, Hopf bifurcation and BT bifurcation using examples. Finally we will talk about predator - prey model and few bifurcations we can see in this model. - Oct. 23, 2019, 4pm, UH2210. A pre-talk for the colloquium talk.
Snacks will be served at 3:30pm in the coffee room (UH2060).Title: Objects, families and spaces of shapes: Introduction to moduli spaces and Teichmuller spaces
Abstract: The theory of moduli spaces, very broadly, is a very deep and modern treatment of Riemann's classification problem of geometric 'objects'. This theory involves and builds connections between several branches of mathematics such as algebraic geometry, algebraic topology, differential geometry and algebraic number theory.
In this talk, we give a gentle introduction to the moduli problem, moduli space of curves and Teichmuller space of Riemann surfaces. On the way we will briefly explain what Teichmuller theory is about. The exposition will be introductory and mostly intuitive, rather than a rigorous treatment of the subject. - Oct. 16, 2019, 4pm, UH2210. A talk by Kursat Yilmaz, 1st year PhD student.
Snacks will be served at 3:30pm in the coffee room (UH2060). (continuation of the talk)
- Oct. 2, 2019, 4pm, UH2210. A talk by Kursat Yilmaz, 1st year PhD student.
Ice cream and coffee will be served at 3:30pm in the coffee room (UH2060).He will give a brief information about topological surgery in 3-dimensional manifolds (after giving a basic definition of manifold), and show some surgery diagrams. He will also show some basic handle slide moves to show that we can pass from one diagram to another without changing the ambient manifold.
- April 26, 2019, Shoemaker lecture series.
Efim Zelmanov, FIELDS medal 1994. Math lecture (FH 2100, 4-5pm)
and General audience lecture (McQuade Law Aud., 7-8pm).
- April 17, 2019, 4pm, UH 4170. A talk by Brian Grove (undergraduate student) on recurrence sequences. He will speak about some of his own findings too.
- April 3, 2019, 4pm, UH 4170. A talk by Khursed Ansari (graduate student).
Title: Intro to Weyl Algebra
Abstract: in this talk , I will define Weyl algebra and discuss some of its properties, for example Weyl algebra is simple ring . Then I will define Bernstein filtration and associated graded ring and show that graded ring is polynomial ring in 2n variables. - March 20, 2019, 4pm, UH 4170. A talk by Prof. Dr. Qin Shao. She will be giving a talk about data science.
- February 13, 2019, 4pm, UH 4170. A talk by Prof. Amrita Acharyya, based on the paper Topology of Finite Graphs, by J.R. Stallings.
- December 5, 2018, 4pm, UH 4170. A talk by Prof. Gerard Thompson. He will be talking about a group representations.
- November 28, 2018, 4pm, UH 4170. A talk by Prof. Trieu Le. How I think about my son's math homework
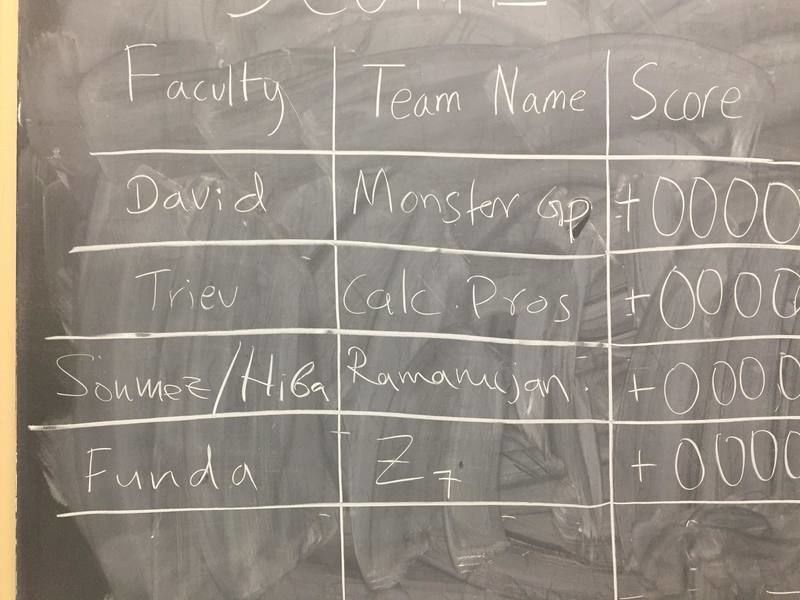
- Math trivia night, November 11, 2018: